HashTables

Maps and Sets provide a clean interface for accessing or looking up the elements within them. There are a number of different ways in which they can be implemented, but the most common one uses a technique known as hashing.

Q: What is Hashing and what makes it so special?
A: A program usually needs to check through multiple elements in a collection to find a single element, but hashing lets it find items immediately, regardless of the size of the collection!
Q: How does hashing do that?
A: Let's see by implementing a basic HashTable, the hashing structure behind HashSets and HashMaps.

Implementing a HashTable

Let's say you have a set of integer keys which map to values and you want to create a structure that can find and modify the values in constant time.

If your set of keys was just a small range of integers, a HashMap would not be necessary since you could use a simple array to store the values, with the index values of the array as 'keys':

In the above array, 0 'maps' to 4 and 4 'maps' to 7. You can create a new 'mapping' for any key k (where k is less than the array's length) by simply updating k^th cell in the array with the value you want.¹

However, if the range of keys is large, an array would need to use up a lot of memory in order to store everything. For example, it would be very inefficient to create an Array of length 200M (200 Million) just to store the following 7 items:

2, 341, 73, 8265, 234004, 7.4M, 200M

Mini-challenge: Can you think of a simple way to convert the above data so it can be stored in a small array, say of size 10?

Solution
We can use the mod operator % on a number to get a remainder r and store the element in index r of the array. For example, if we did mod 10 on each number, we would get the following remainders:

2, 1, 3, 5, 4, 0, 0

We can then store the values in an array of size 10:

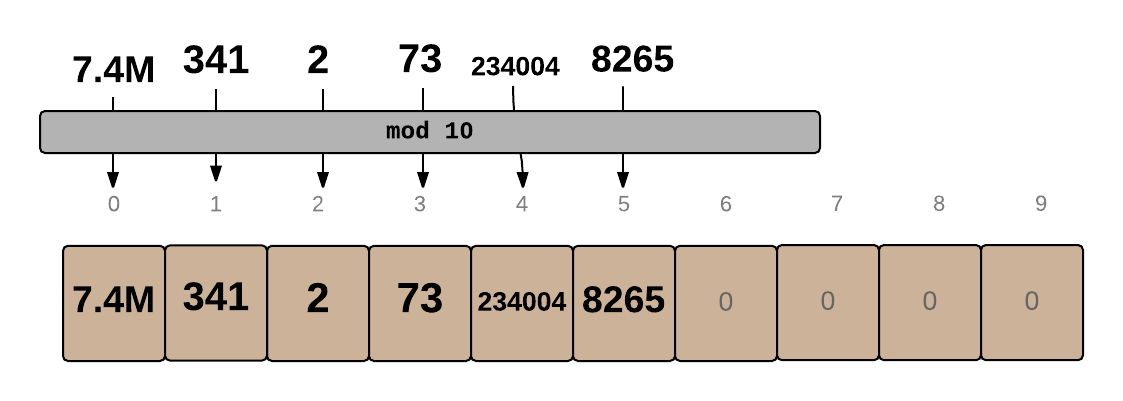
In the above diagram, the actual keys are stored in the array, so it can be used as a HashSet. To create a HashMap, we could just store simple Objects with keys and values.

Note that 200M didn't make it to the array, since the 0 cell was already occupied. When two keys end up at the same index, there's a collision. The simplest way to resolve collisions is to create a List at each location in the array, so multiple items can be stored. As long as collisions are rare, we'll still be able to find every item quickly.

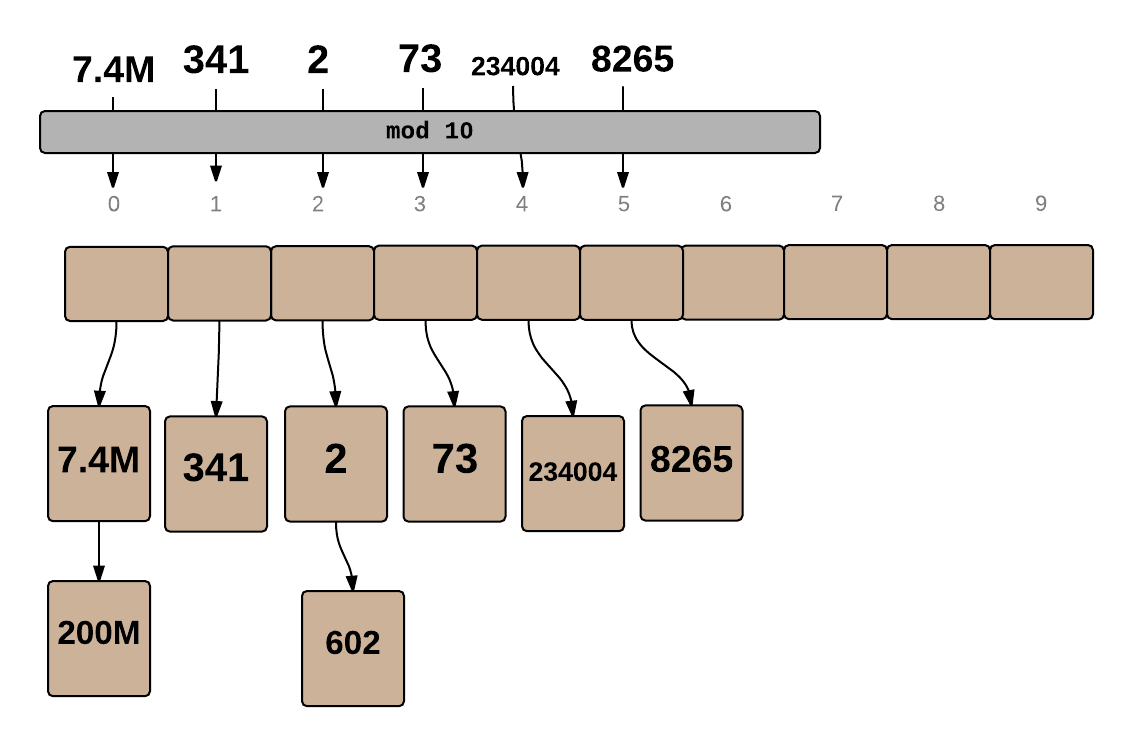
In the above case, for every number n, we did n % 10 to find the location of the element. This function is known as the Hash Function. Real-world hash functions are more complicated, but the purpose is to convert a number of any size to a number contained within a small range of values while avoiding too many collisions.

Q: What if the data we're using as keys is not a number?
A: All data is represented as numbers in some manner in a computer, so the computer can use those numbers in the hash function. The key idea of the hash function is to use the actual value of an item to find the item in an array.

Challenge

1. Create your own list-based hash table with n mod 11 as the hash function for each number n. Always use the absolute value of n.
2. Given a list of numbers, hash them all into the hash table.
3. Print out the numbers in the order that they appear in the hash table. Print all the numbers in each list in the order they were inserted and then go on to the next list.

Guideline
To create the HashTable in Java, create an ArrayList and fill it with empty Lists of Integers.

Sample Input

1
11
12 24 125 5 91 1106 2 1021 29 3536 10

Sample Output

12 24 2 91 125 5 3536 1106 29 1021 10

The hash table will look like this at the end:

0  1  2  3  4  5  6   7   8   9   10  //index
. 12 24 91 125 5 1106 29  . 1021  10  //values
      2       3536

^{1. You can use this array-index approach to optimally solve Duplicate Duplicates.}