Graphs

Graphs

Graphs are important data structures used in many areas, such as mapping the roads of an area, or charting the connection between people on a social network.

Definition
A graph is a set of Nodes and a collection of Edges that connect each pair of Nodes. Here's a simple graph, with Nodes numbered 0 to 5:

Trees are special types of graphs where each Node has one parent and cycles are not allowed. Graphs allow cycles, and there's no hierarchy of parents and children. Nodes can be connected to any number of other Nodes in a graph, or to none of them:

Node 1 is disconnected from the other Nodes

We will deal with ordinary graphs, which are undirected - if you can travel from Node a to Node b, you can also go from Node b to Node a. (Directed graphs do not follow this condition.)

Representing a Graph

A Node in a real-world graph represents something unique, such as a city on a map, or a person in a network. When studying graphs, the nodes can just be labeled with a unique number starting from 0, so they're easy to work with.

There are many ways to represent a graph in a computer. A good structure should balance using space efficiently and performing operations quickly. As seen with Trees, you could represent the data with individual Nodes. However, this wouldn't let you quickly access any Node in the graph. A good alternative is to create an array or list to represent all the nodes. Each cell in the list can then store a list of all the Nodes that are connected to that Node.

For example, the following graph can be represented as shown below:

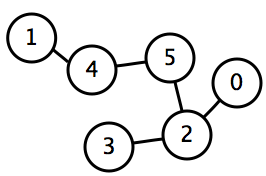
index	list of connected nodes
0	2
1	4
2	5 0 3
3	2
4	1 5
5	4 2

This shows the connections between nodes 0 and 2, nodes 1 and 4, etc.

Challenge

You will be given lists of numbers as input based on the above format. Create a graph structure from the input or use the provided boilerplate. Then start from Node 0 and repeatedly visit and print the next connected node until you reach Node 4.

While Nodes don't necessarily have a set order for their connections, in this challenge you should go to the first Node in the list of input. For example, in the above graph, go from 0 to 2 to 5 to 4 and then stop.

Input format
The first line of input will contain T, the number of tests cases. T cases will follow, with each case consisting of multiple lines:

• A number n on the first line, representing the number of Nodes.
• n lines follow, with each line i representing the Nodes that are connected to Node i.

Sample Input
Hover over numbers for more info

1
6
2
4
5 0 3
2
1 5
4 2

Sample Output

0 2 5 4

Optional boilerplate code is provided for Java which converts the input to an ArrayList of ArrayLists. Similar boilerplate is provided for Python, Ruby and Javascript.