Depth-First Search

To do something useful with graphs, you need to be traverse them systematically to find connections and paths. Depth-First Search (DFS) traverses through a graph's nodes by going as far as possible in one direction before backtracking. (See Backtracking for a non-tree example.)

In this Algorithm visualizer you can view the graph as a logical chart or as a list of lists. Pick a start vertex, and then click Run DFS to see the algorithm in action!

DFS Algorithm

DFS goes through a graph as far as possible in one direction before backtracking to other nodes. DFS is similar to the pre-order tree traversal, but you need to make sure you don't get stuck in a loop. To do this, you'll need to keep track of which Nodes have been visited. Before clicking below, see if you can figure out a recursive algorithm to print out a graph in DFS order.

Q: If you're using actual Nodes for your graph, you can mark them as visited, but how will you track visits if you're just using lists of numbers?
A: You can use an array of booleans that keeps track of which Nodes have been visited.

Challenge

Create a graph from the given input and Run through it with a Depth-first-search. Print out the nodes in the order you first visit them, with each graph's printout on its own line. Visit the first adjacent Node in the input before going on to the other nodes.

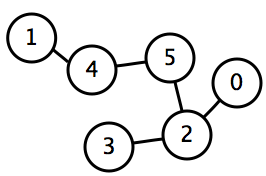
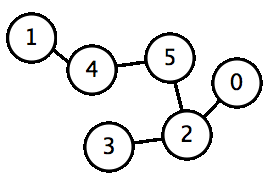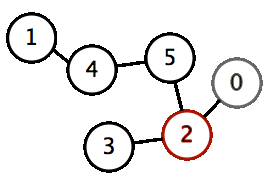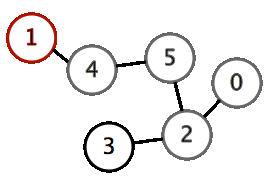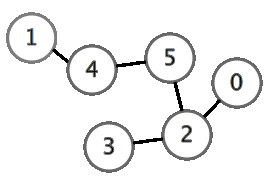
Input format
The input is the same as the last challenge. The first line of input will contain T, the number of tests cases. T cases will follow, with each case consisting of multiple lines:

• A number n on the first line, representing the number of Nodes.
• n lines follow, with each line i representing the Nodes that are connected to Node i.

Sample Input

1
6
2
4
5 0 3
2
1 5
4 2

Sample Output

0 2 5 4 1 3

Explanation
This is the DFS order of the graph, as shown in the above animation.

For this challenge, visit equivalent nodes in the same order as their line of input. For example, 5 comes before 3 in the output since it was before 3 in the input.

Using DFS

DFS is the natural way to solve certain problems, such as solving a maze. You explore a path until you reach a dead-end, and then you backtrack to check another path. You can try a maze-type challenge with the explorer escape. DFS can also be used to search a graph when you don't need to go through it one level at a time. For example, you can modify DFS to Find the Cycles in a graph.