Breadth-First Search

DFS vs. BFS

DFS is a simple algorithm, but the path it finds to a Node may not be the shortest. In cases where that matters, you'll want to use Breadth-First Search (BFS) instead. Instead of following a path all the way to the end, BFS goes through a graph one level at a time:

You can view BFS in action with this Algorithm visualizer. Pick a start vertex and then click Run BFS.

BFS Algorithm

BFS begins at one node in a graph and visits all the neighboring nodes. It then goes to each of those neighbors to explore their unvisited neighbors in order. So it goes through the entire graph one level at a time, until the whole graph has been visited.

DFS was simple to implement, since you could use recursion to stack up the Nodes. However, BFS goes through the Nodes one level at a time, so you need a structure to keep track of the next nodes to be processed.

Q: What structure can be used to access items in the order they were put in?
A: A Queue (such as a LinkedList).

Before clicking below, see if you can describe of an Algorithm that uses a Queue to print the Nodes in a Graph in BFS order.

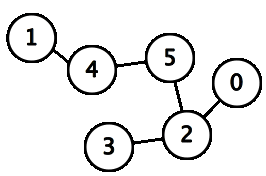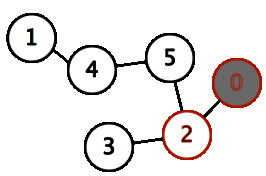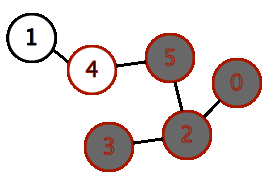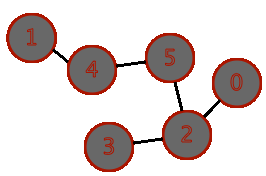
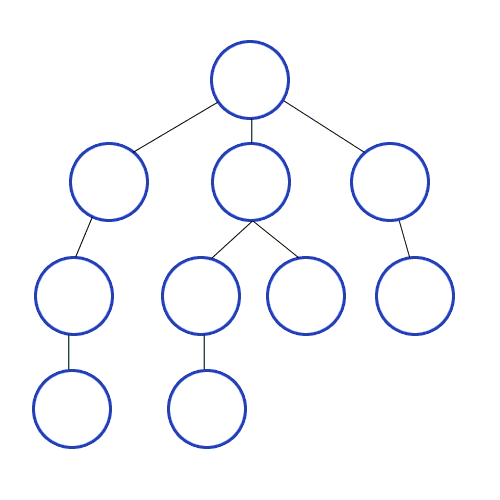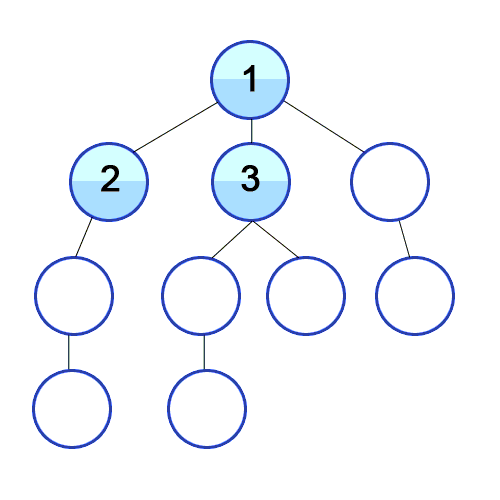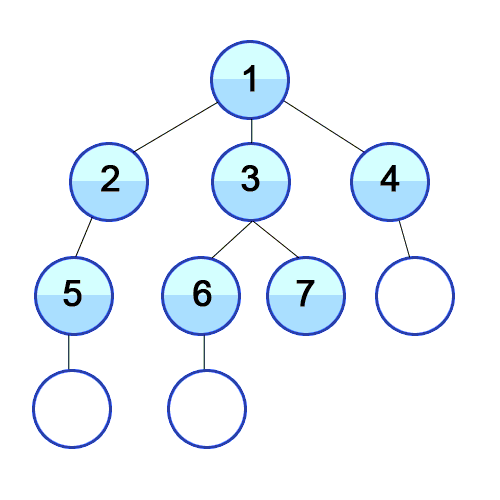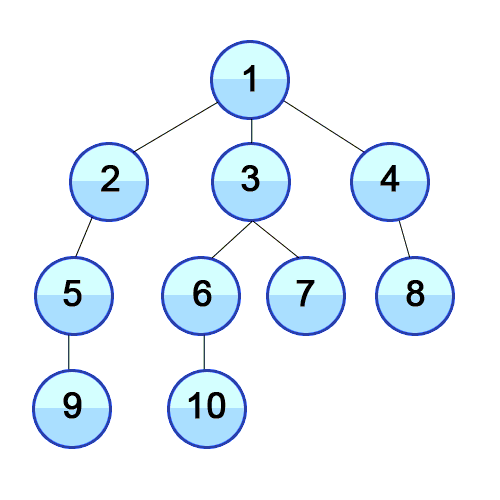
BFS on sample input. Marks node red when visited, and grey when finished with.

Challenge

Create a graph from the given input and print it out in BFS order.

Input/Output Format
The Input and output format are the same as the previous graph challenges. Print out the graph in BFS order, with each graph on its own line. (You can use the provided boilerplate code to get a graph as a list of lists.)

Sample Input
Hover over numbers for more info

1
6
2
4
5 0 3
2
1 5
4 2

Sample Output

0 2 5 3 4 1

Explanation
This is the order of the BFS search, as seen in the above animation.

For this challenge, visit equivalent nodes in the same order as their line of input. For example, 5 comes before 3 in the output since it was before 3 in the input.

Using BFS

BFS can be used whenever you need to search a graph, such as in the Connected Components challenge. BFS is necessary to search a graph one level at a time, such as finding the shortest path to a node. BFS is also necessary for searching a graph without a clear ending, which will be covered in future AI challenges.